数独技巧教程
数独入门教程
从零开始了解数独规则和基本概念,适合首次接触数独的玩家。通过简单易懂的图文解析,快速掌握游戏基础。

数独规则与基础
了解数独的基本规则和游戏历史,为深入学习奠定基础。
数独规则图文说明
数独的基本规则非常简单:每一行、每一列以及每个3x3的宫格内必须包含数字1到9,且不能重复。
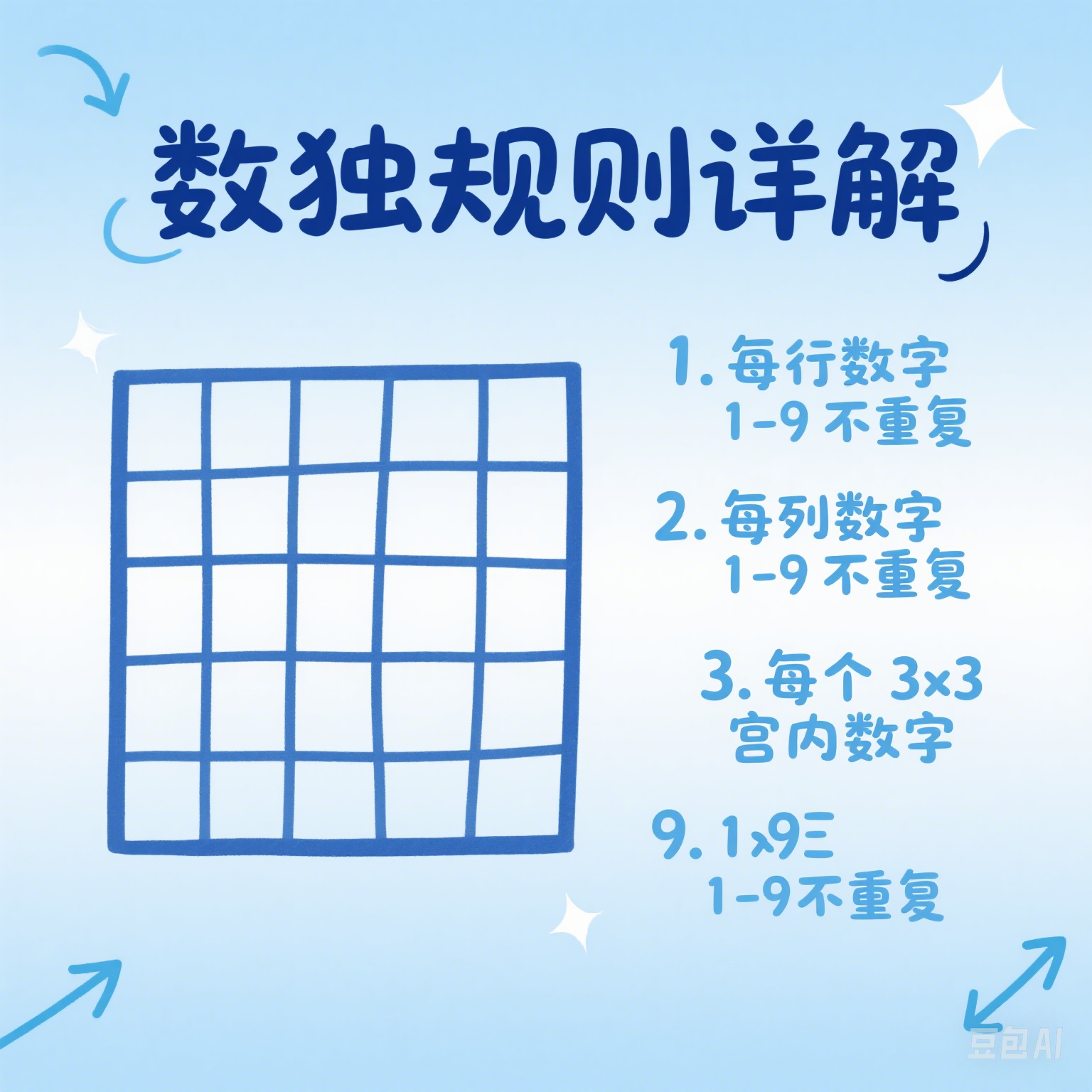
行规则:每一行必须包含1-9的数字,不能重复。
列规则:每一列必须包含1-9的数字,不能重复。
宫规则:每个3x3宫格必须包含1-9的数字,不能重复。
解题过程中,需要依据上述三个规则,逐步确定每个单元格的数值。
数独入门基础
数独游戏虽然看似复杂,但掌握了基本技巧后,解题会变得轻松有趣。 初学者可以从简单难度开始,通过实践逐步提升解题能力。

先找出那些只有一个可能解的单元格,也就是应用唯一候选数法。
使用扫描法寻找行、列或宫中只能放置特定数字的位置。
反复应用这些基础技巧,直到无法继续前进或完成解题。
初级解题技巧
掌握数独基础解题方法,轻松应对简单到中等难度的数独题目。这些技巧是解决大多数数独谜题的关键基础。

基础解题技巧
掌握唯一候选数法、候选数删减法等基础技巧,解决简单到中等难度的数独。
扫描法
扫描法是最基础的数独解题技巧,通过行、列、宫的交叉扫描来确定唯一可能的数字位置。
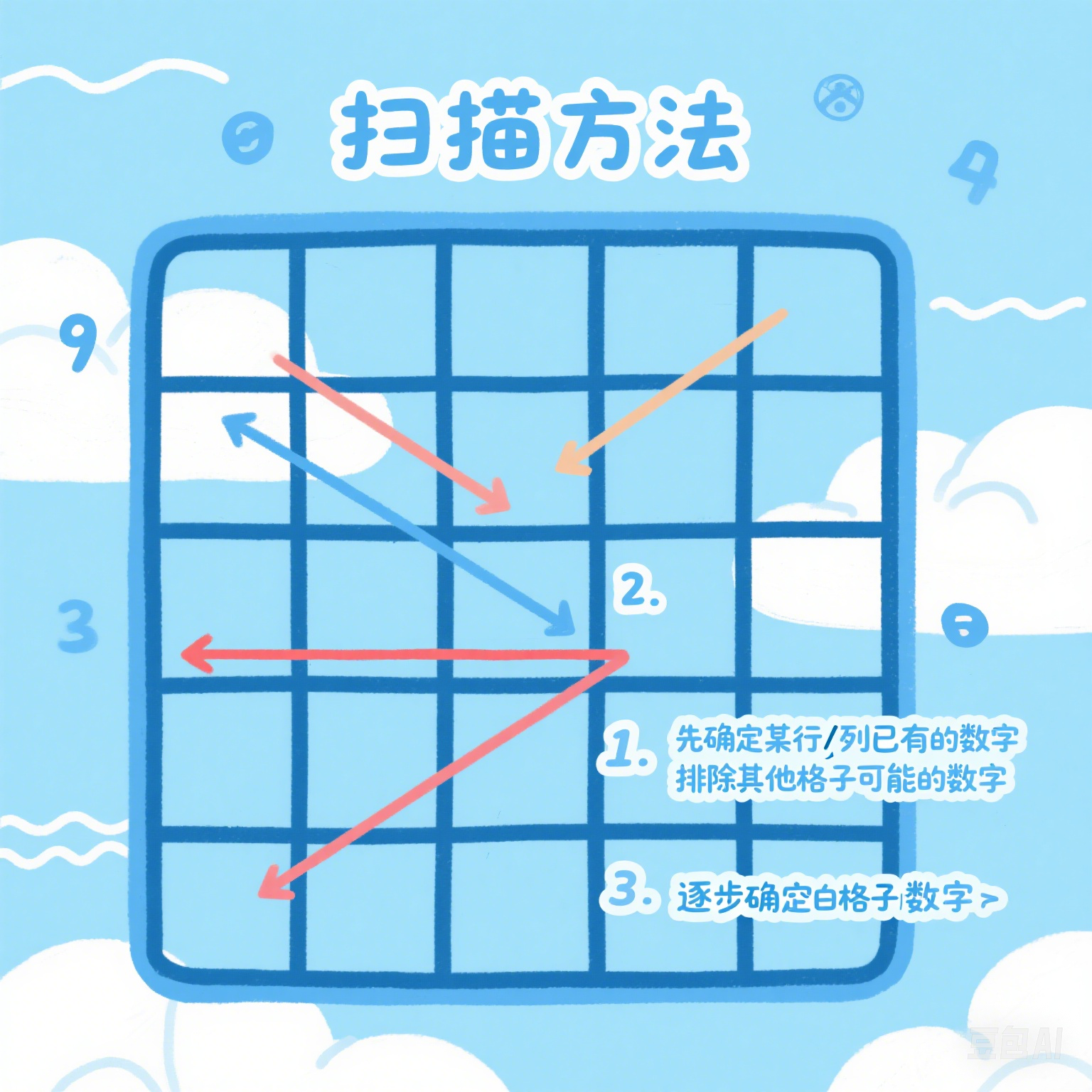
选择一个数字(比如数字1),从第一行开始扫描,找出此行可能放置该数字的所有位置。
继续扫描相关的列和宫,排除不可能的位置。
如果最终只剩下一个可能的位置,那么该数字就确定在此位置。
对所有数字(1-9)和所有行、列、宫重复此过程。
唯一候选数法
当一个单元格只有一个可能的数字时,该数字必然填入此单元格,这就是唯一候选数法。

确定每个空格的所有候选数(根据行、列、宫规则排除已有数字)。
找出只有一个候选数的单元格。
填入该候选数,并更新相关单元格的候选数列表。
候选数删减法
通过行、列、宫的规则,删除不可能的候选数,从而简化解题过程。

为每个空格标记所有可能的候选数(1-9中符合规则的数字)。
当某个单元格确定一个数字后,从同行、同列、同宫的其他单元格中删除该数字的候选标记。
不断重复此过程,直到某些单元格的候选数减少为1,从而确定该单元格的数字。
宫内摒除法
当某个数字在一个3×3宫内只能出现在特定的行或列中时,可以排除该行或列在其他宫中的相同候选数。

分析某个3×3宫内特定数字的可能位置。
如果该数字只能出现在宫内的某一行(或列)中,则该行(或列)的其他宫中不可能出现此数字。
删除该行(或列)其他宫中的对应候选数。
中级解题技巧
学习更进阶的数独解题策略,突破困难级别的数独谜题瓶颈。这些技巧能帮助你解决大部分困难级数独。

中级解题策略
学习明暗对子法、X-Wing等中级技巧,突破困难级别的数独谜题。
明暗对子法图解
对子法是中级数独解题的重要技巧,分为明对子(Naked Pairs)和暗对子(Hidden Pairs)。 当掌握了这些技巧后,可以大幅提升解决中等难度数独的能力。

明对子:当同一行、列或宫中有两个单元格的候选数完全相同且只有两个时,这两个候选数只能出现在这两个单元格中,可以从同一行、列或宫的其他单元格中删除这两个候选数。
X-Wing技巧图解
X-Wing是一种强大的高级解题技巧,适用于中高难度的数独谜题。
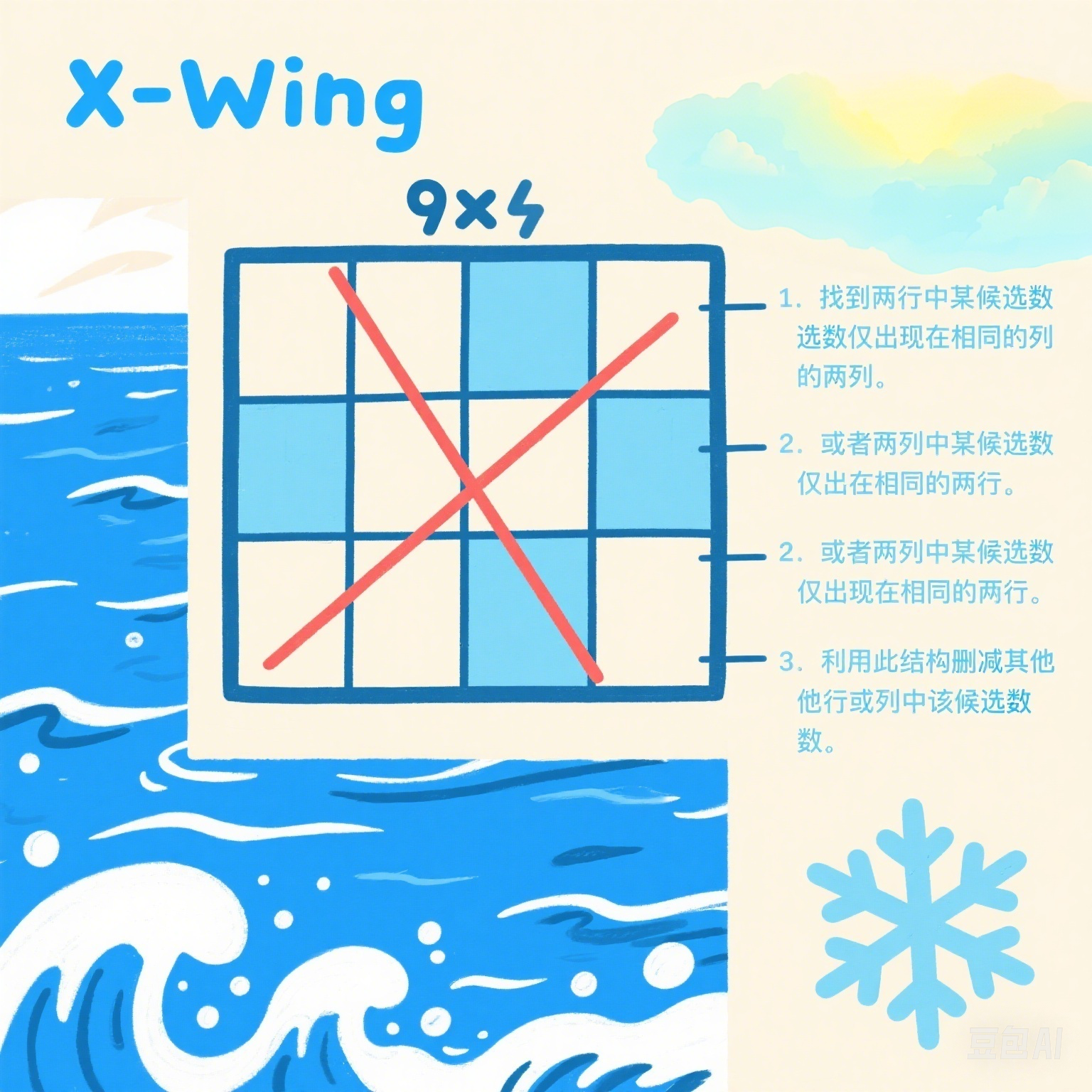
当某个数字在两行中各自仅出现在相同的两列位置上时,形成一个矩形(如同字母X)。
此时,这两列的其他行中可以排除该数字作为候选数。
同理,当某个数字在两列中各自仅出现在相同的两行位置上时,这两行的其他列中可以排除该数字。
高级解题技巧
探索最复杂的数独解题技巧,挑战专家级数独谜题。掌握这些方法后,几乎没有你解不开的数独难题。

高级解题技巧
探索XY-Wing、Swordfish等高级技巧,挑战专家级数独谜题。
XY-Wing技巧图解
XY-Wing是一种高级解题技巧,对于解决困难和专家级数独非常有效。
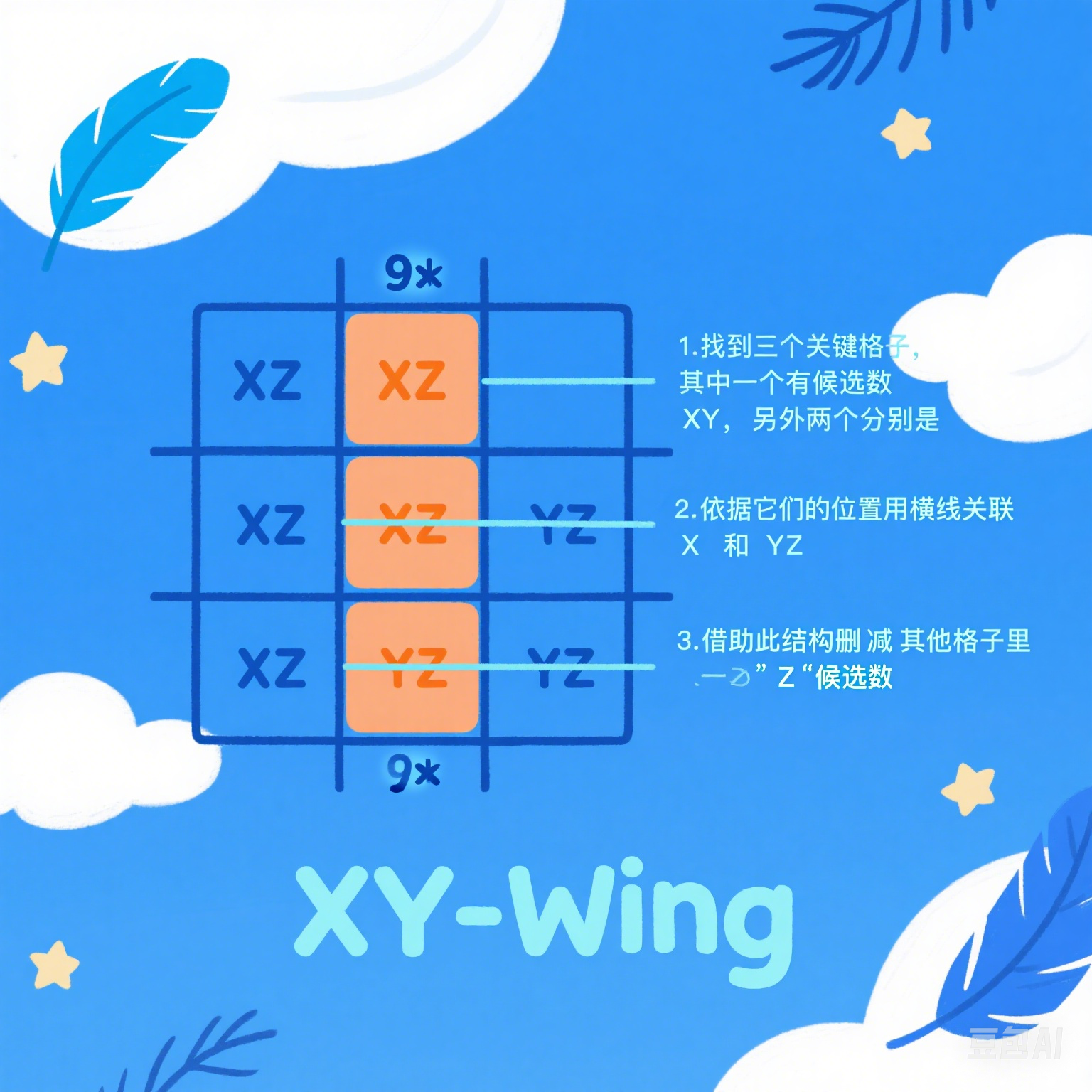
寻找一个只有两个候选数(XY)的单元格作为"枢纽"。
找到两个与枢纽相关(同行、同列或同宫)的单元格,它们分别有两个候选数(XZ和YZ),并且它们都包含一个与枢纽相同的候选数和另一个共同的候选数Z。
这三个单元格形成"Y"形状,此时可以从能同时看到后两个单元格的所有单元格中删除候选数Z。
Swordfish技巧图解
Swordfish技巧是X-Wing的扩展版本,涉及三行三列的交叉模式。

寻找三行中某个数字的候选位置仅限于三列之内。
这形成一个3×3的矩阵(最多有9个单元格,但实际的候选位置可能少于9个)。
此时,可以从这三列中、不属于这三行的其他单元格中删除该数字的候选标记。
同理,当三列中某个数字的候选位置仅限于三行之内,可以从这三行中、不属于这三列的其他单元格中删除该数字。
着色法图解
着色法(Coloring)是一种强大的可视化技巧,通过标记互相关联的候选数来找出矛盾或确定解。

找出某个数字的所有候选位置,将相互关联(同行、列或宫)的候选位置用两种颜色交替标记。
如果同一颜色的两个标记出现在互相关联的位置,则出现矛盾,表明该颜色标记的所有位置都不可能是该数字。
如果能确定一个颜色标记的位置不正确,则另一种颜色标记的所有位置必定正确。
当某个位置可以同时看到两种颜色标记,则该位置可以删除此数字的候选标记。